jean-marie laugier MCF Université de Provence Marseille -FRANCE http://www.up.univ-mrs.fr/~laugierj/ laugierj@up.univ-mrs.fr case 1 Université de Provence 13331 Marseille cedex tel 04 91 10 61 76 / 62 76 (33 491 106 176)

.

Les constructions classiques sur la réfraction :

On choisit A et I avec des vitesses de propagation v1 et v2 dans chaque milieu., les rayons des cercles sont proportionnels à v1 et v2, la construction vérifie la relation : v2/v1= sin(i2)/sin(i1) ou sin(i1)/v1=sin(i2)/v2

Les triangles IBH et IXH sont rectangles par construction
IHB = NIB = i2 et IHX = NIX = i1
IB/IH = sin(IHB) et IX/IH = sin(IHX)
IB/IX = sin(IHB)/sin(IHX)
v2/v1 = sin(i2)/sin(i1)
sin(i1)/v1 = sin(i2)/v2

Cette deuxième construction, plus simple, utilise les cercles des indices :
On choisit A et I avec les indices n1 et n2 dans chaque milieu, les rayons des cercles sont proportionnels à n1 et n2, la construction vérifie la relation : n1*sin(i1)=n2*sin(i2)

IH = IB * sin(i2) = IB' * sin(i1)
IB/IB' = sin(i1) / sin(i2) = n2/n1

n1*sin(i1)=n2*sin(i2)

Chemin optique :

Position du problème

Les lois de Snell-Descartes sur la réfraction sont établies à partir du principe de Fermat. Ce principe est énoncé en 1657 par Pierre de Fermat lui-même sous la forme "La lumière se propage d'un point à un autre sur une trajectoire telle que la durée du parcours soit minimale".

Cet énoncé ne permet pas de tracer simplement un rayon lumineux qui passe par deux points situés dans deux milieux d'indices différents, séparés par un dioptre plan.
Par exemple, si les données sont les points A et B, comment tracer les rayons AI et IB tels que le "la durée du parcours soit minimale" ou le chemin optique soit minimal ?

fig1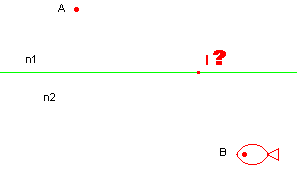

Généralement, on se donne les points A et I, puis connaissant les indices n1 et n2, on trace AI et IB tels que : n1 sin(i1)=n2 sin(i2) D'autre part, seules les directions de AI et IB sont déterminées, on n'a pas l'image de B.

fig2

Si le point A représente le pêcheur, comment déterminer géométriquement la position de l'image B' du point B et du poisson ?
Cabri Géomètre II peut nous aider à résoudre ce problème, à condition de le reformuler d'une manière vraiment géométrique, y compris pour déterminer la positon de l'image de B.

fig3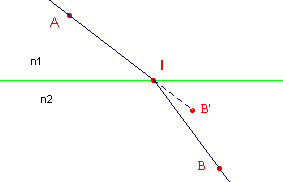

On peut commencer par poser le problème sous la forme la plus proche de l'énoncé du principe de Fermat, avec le chemin optique minimal.

A et B sont le pêcheur et le poisson C est défini par OC= n * OB (n=n2/n1) sur la droite DV On cherche le chemin optique L= AIB minimal avec ; L=AI +n * IB La création du point C est naturelle en considérant que si le point A est sur la droite DV, alors I et O sont confondus et C est tel que OC= n * IB.

fig4

Pour calculer le chemin L, on trace un cercle C1 de centre A de rayon AI puis un cercle C2 de centre I de rayon n * IB, en utilisant une homothétie de rapport n (point B').

L est la distance AX

fig5

Lorsque le point I se déplace sur le dioptre, l'ensemble des cercles de centre I et de rayon n * IB =IB' (outil "lieu" de Cabri Géomètre) fait apparaître une ellipse qui a un demi grand axe de longueur OC = n * OB

On voit que X s'approche de l'ellipse dessinée par le faisceau de cercles lorsque le point I se déplace sur le dioptre.

fig6

On calcule la longueur du chemin optique L avec AI et IB' avec les fonctions "Distance" et "Calculatrice".

On trace la perpendiculaire à AX en X.

L est minimal lorsque la droite XP est tangente à l'ellipse. Cette ellipse est définie par les foyers B et son symétrique par rapport au dioptre et passe par le point C.

fig7

On peut alors tracer l'ellipse de demi grand axe OC et de foyer B (en utilisant la macro "Coniques 2 foyers 1 point")
et sa tangente X'T en X', intersection de la droite AI avec l'ellipse (en utilisant la macro "Tangente en un point d'une conique")

En déplaçant I, on voit bien que X'T et XP sont confondues lorsque le chemin optique L est minimal.

fig8

D'où un nouvel énoncé du problème... Soient : DH une droite horizontale A un point au-dessus de cette droite B un point au-dessous de cette droite DV la droite perpendiculaire à DH qui passe par B C un point de DV au-dessous de la droite C' le symétrique de C par rapport à DH g l'ellipse de grand axe CC' et de foyer B X un point de cette ellipse Question:

Trouver X tel que la droite AX a sa perpendiculaire en X confondue avec la tangente à l'ellipse en X,
ou bien
Trouver la courbe G passant par A et X telle que la droite AX a sa perpendiculaire en X confondue avec la tangente à l'ellipse g en X.

ou bien
Trouver la courbe G passant par A et X telle que la droite AX soit normale à l'ellipse g en X.

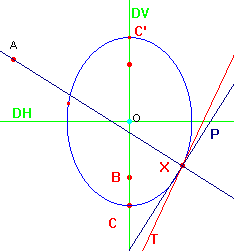L'hyperbole d'Apollonius répond à la question posée ici et plus généralement permet de construire les normales à une conique g passant par un point A .

fig 9

Constructions avec l'hyperbole d'Appolonius :

On obtient ainsi la figure 10,

fig10

avec bien entendu, la vérification de la loi de Snell-Descartes pour la réfraction avec les constructions de Descartes (cercles des indices) fig 11 et de Huygens (cercles des vitesses) fig 12.
En effet, si on demande à Cabri Géomètre avec la propriété "Appartient ?" si le point E est sur la droite perpendiculaire au dioptre passant par D, la réponse est : "Le point est sur l'objet". De même, la perpendiculaire en X à AI coupe le dioptre en H. Cabri trouve que H appartient à la normale en B à IB.

Snell Descartes , Fermat et cercles des indices

fig11

Huygens , Fermat et cercles des vitesses

fig12

Image d'un point

Avec cette construction, on obtient la direction du rayon AI mais on n'obtient pas encore l'image de B perçu par l'observateur situé au point A. Pour obtenir l'image du point B, il faut au moins deux rayons.
On prend alors un point A' voisin de A (distance exagérée sur la figure 13), par exemple sur la perpendiculaire à AI, et on refait la même construction qui défini un nouveau point I'.
L'intersection des rayons AI et A'I' donne la position de l'image B' du point B.

fig13
macro image d'un point

Image d'un objet étendu

On peut alors passer à l'image d'un objet étendu (poisson)

Erreurs de visée (harpon+poisson)

Le point de vue du poisson : image du pêcheur et de la canne à pêche.

les deux points de vue

cas d'un problème 3D

Pour la configuration suivante

Applications en classe :

mesures d'un indice : un peu de CabriJava

régression linéaire (pour aller un peu plus loin)

analogie avec un maître nageur qui doit sauver un nageur en perdition

A résoudre

Equivalence Appolonius/Huygens:

Soit une ellipse définie par ses foyers F1 F2 et le point M sur le grand axe.
Soit un point A sur cette ellipse et sa tangente à l'ellipse T .
Cette tangente coupe la droite YY' qui porte le petit axe de l'ellipse en H.
Soit D la droite qui passe par H et F1.
PA et PF sont les normales en A et F1 aux droites T et D

Montrer que les droites PA et PF sont concourantes en K sur la droite YY' .

Montrer que KA/KF1 = OM/OF1

Dioptre sphérique

On recommence la construction de Fermat avec un dioptre sphérique, le lieu des cercles ne fait plus apparaitre une ellipse mais...